
Zadanie Połączenia (pol)
Pomóż nam usprawnić bazę zadań!
Połączenia
Limit pamięci: 32 MB
Ministerstwo Infrastruktury Bajtocji postanowiło stworzyć program
pozwalający szybko obliczać długości tras między dowolnymi miastami.
Nie byłoby w tym nic dziwnego, gdyby nie fakt, iż mieszkańcy Bajtocji
nie zawsze szukają najkrótszej trasy. Zdarza się, że
pragną dowiedzieć się o 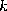 -tą co do długości najkrótszą trasę.
Dopuszczamy zapętlenia tras, tzn. takie trasy, na których
miasta powtarzają się.
-tą co do długości najkrótszą trasę.
Dopuszczamy zapętlenia tras, tzn. takie trasy, na których
miasta powtarzają się.
Przykład
Jeśli między dwoma miastami istnieją 4 trasy o długościach: 2, 4, 4 i 5, to najkrótsze połączenie ma długość 2, drugie co do długości 4, trzecie 4, a czwarte 5.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis sieci dróg Bajtocji oraz zapytania dotyczące długości tras przejazdu,
- obliczy i wypisze na standardowe wyjście odpowiedzi do wczytanych zapytań.
Wejście
W pierwszym wierszu standardowego wejścia
zapisane są dwie dodatnie liczby całkowite  i
i 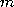 oddzielone pojedynczym odstępem,
oddzielone pojedynczym odstępem,
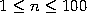 ,
, 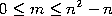 .
Są to odpowiednio liczba miast w Bajtocji oraz
liczba dróg łączących miasta.
Miasta są ponumerowane od
.
Są to odpowiednio liczba miast w Bajtocji oraz
liczba dróg łączących miasta.
Miasta są ponumerowane od 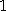 do
do  .
.
W każdym z kolejnych 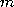 wierszy znajdują się po trzy liczby całkowite
oddzielone pojedynczymi odstępami:
wierszy znajdują się po trzy liczby całkowite
oddzielone pojedynczymi odstępami:  ,
, 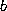 i
i  ,
,
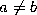 ,
, 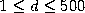 .
Każda taka trójka opisuje jedną, jednokierunkową drogę długości
.
Każda taka trójka opisuje jedną, jednokierunkową drogę długości  umożliwiającą przejechanie z miasta
umożliwiającą przejechanie z miasta  do
do 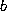 .
Dla każdych dwóch miast istnieje co najwyżej jedna droga
umożliwiająca przejazd w danym kierunku.
.
Dla każdych dwóch miast istnieje co najwyżej jedna droga
umożliwiająca przejazd w danym kierunku.
W kolejnym wierszu znajduje się jedna liczba całkowita 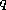 ,
,
 , oznaczająca ilość zapytań.
W kolejnych
, oznaczająca ilość zapytań.
W kolejnych 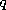 wierszach są zapisane zapytania, po jednym w wierszu.
Każde zapytanie to trzy liczby całkowite
oddzielone pojedynczymi odstępami:
wierszach są zapisane zapytania, po jednym w wierszu.
Każde zapytanie to trzy liczby całkowite
oddzielone pojedynczymi odstępami:  ,
,  i
i 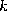 ,
,
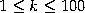 .
Zapytanie takie dotyczy długości
.
Zapytanie takie dotyczy długości 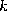 -tej najkrótszej trasy
z miasta
-tej najkrótszej trasy
z miasta  do miasta
do miasta  .
.
Wyjście
Twój program powinien wypisywać odpowiedzi na wczytane zapytania
na standardowe wyjście, po jednej odpowiedzi w wierszu.
W 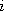 -tym wierszu powinna zostać wypisana
odpowiedź na
-tym wierszu powinna zostać wypisana
odpowiedź na 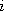 -te zapytanie - jedna liczba całkowita równa
szukanej długości trasy lub
-1, gdy taka trasa nie istnieje.
-te zapytanie - jedna liczba całkowita równa
szukanej długości trasy lub
-1, gdy taka trasa nie istnieje.
Przykład
Dla danych wejściowych:
5 5 1 2 3 2 3 2 3 2 1 1 3 10 1 4 1 8 1 3 1 1 3 2 1 3 3 1 4 2 2 5 1 2 2 1 2 2 2 1 1 2
poprawną odpowiedzią jest:
5 8 10 -1 -1 3 6 -1
Autor zadania: Krzysztof Sikora.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English