
Zadanie Obława (obl)
Pomóż nam usprawnić bazę zadań!
Obława
Limit pamięci: 32 MB
Jak powszechnie wiadomo, w Bajtocji jest  miast połączonych
miast połączonych 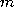 dwukierunkowymi drogami.
W tym zadaniu jednak drogi służą nie tylko prawym obywatelom, lecz również pewnemu groźnemu przestępcy.
dwukierunkowymi drogami.
W tym zadaniu jednak drogi służą nie tylko prawym obywatelom, lecz również pewnemu groźnemu przestępcy.
Od pewnego czasu w Bajtocji trwa obława, której celem jest doprowadzenie go przed oblicze karzącej ręki sprawiedliwości.
Na razie jednak ów wykolejeniec nadal cieszy się niezasłużoną wolnością.
Dnie spędza on ukryty w jednym z miast, natomiast nocą potajemnie przedostaje się jedną z 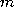 dróg do sąsiedniego miasta.
Nigdy nie pozostaje przez dwa kolejne dni w tym samym mieście.
dróg do sąsiedniego miasta.
Nigdy nie pozostaje przez dwa kolejne dni w tym samym mieście.
Obecnie o jego lokalizacji nie wiadomo nic. Do akcji wkracza jednak Porucznik Bajtewicz, który nie takie orzechy rozgryzał. W ciągu dnia potrafi on przeczesać jedno miasto i bez trudu dopadnie szubrawca, o ile będzie on właśnie w tym mieście. Za to nocą, przy pomocy helikoptera może przedostać się do dowolnego innego miasta. Obławę utrudnia fakt, że gangster z góry dokładnie wie, gdzie którego dnia znajdzie się Porucznik, dlatego postanowił, że będzie wymykał się Bajtewiczowi tak długo, jak to będzie możliwe.
Czy Porucznik Bajtewicz ma szansę dopaść złoczyńcę? Mówiąc ściślej, czy istnieje taka strategia Porucznika, która gwarantuje mu złapanie kryminalisty? Jeśli tak, to ilu minimalnie dni potrzeba, aby to osiągnął?
Wejście
Pierwszy wiersz wejścia zawiera jedną liczbę całkowitą 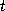 (
(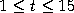 ) oznaczającą liczbę przypadków testowych, które są kolejno opisane w dalszej części wejścia.
Opis jednego przypadku testowego rozpoczyna się dwoma liczbami całkowitymi
) oznaczającą liczbę przypadków testowych, które są kolejno opisane w dalszej części wejścia.
Opis jednego przypadku testowego rozpoczyna się dwoma liczbami całkowitymi  i
i 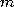 (
(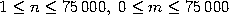 ) oznaczającymi odpowiednio liczbę miast i liczbę dróg łączących miasta.
Miasta ponumerowane są liczbami od
) oznaczającymi odpowiednio liczbę miast i liczbę dróg łączących miasta.
Miasta ponumerowane są liczbami od 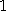 do
do  .
Kolejne
.
Kolejne 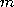 wierszy zawiera po dwie liczby całkowite
wierszy zawiera po dwie liczby całkowite 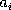 i
i 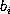 (
(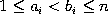 ), które oznaczają, że miasta
), które oznaczają, że miasta 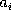 i
i 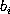 są połączone dwukierunkową drogą.
Żadna para miast nie jest połączona więcej niż jedną bezpośrednią drogą, a ponadto za pomocą sieci dróg da się dostać z każdego miasta do dowolnego innego.
są połączone dwukierunkową drogą.
Żadna para miast nie jest połączona więcej niż jedną bezpośrednią drogą, a ponadto za pomocą sieci dróg da się dostać z każdego miasta do dowolnego innego.
Wyjście
Dla każdego przypadku testowego pierwszy wiersz wyjścia powinien zawierać napis TAK, jeśli istnieje strategia pozwalająca złapać gangstera, zaś NIE w przeciwnym przypadku.
Drugi wiersz powinien zawierać dokładnie jedną liczbę całkowitą.
Jeśli strategia istnieje, liczba ta powinna być równa minimalnej liczbie dni, których potrzebuje Porucznik na złapanie bandyty, przy założeniu, że zbrodniarz z góry zna jego ruchy. W przeciwnym przypadku drugi wiersz powinien zawierać liczbę 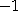 .
.
Ocenianie
Za udzielenie niepełnych odpowiedzi, możesz otrzymać część punktów za każdy test. Rozwiązanie, które poprawnie stwierdza, czy strategia Porucznika istnieje, jednak wypisze niepoprawną liczbę w drugim wierszu, otrzyma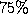 punktów za test.
Wymagamy jedynie, by wypisana liczba była mniejsza niż
punktów za test.
Wymagamy jedynie, by wypisana liczba była mniejsza niż 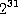 co do wartości bezwzględnej.
Dodatkowo, rozwiązania poprawne jedynie dla pewnych szczególnych klas przypadków testowych, mają szansę dostać niezerową liczbę punktów.
co do wartości bezwzględnej.
Dodatkowo, rozwiązania poprawne jedynie dla pewnych szczególnych klas przypadków testowych, mają szansę dostać niezerową liczbę punktów.
Przykład
Dla danych wejściowych:
3 2 1 1 2 3 3 1 2 2 3 1 3 4 3 1 2 3 4 2 4
poprawną odpowiedzią jest:
TAK 2 NIE -1 TAK 4
Wyjaśnienie do trzeciego przypadku testowego: Porucznik może przeczesywać kolejno miasta o numerach 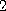 ,
,  ,
,  i
i 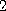 . Wówczas niegodziwiec nie ma szans na ucieczkę.
. Wówczas niegodziwiec nie ma szans na ucieczkę.
Autor zadania: Tomasz Kociumaka.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English