
Zadanie Listonosz (lis)
Pomóż nam usprawnić bazę zadań!
Listonosz
Limit pamięci: 64 MB
Listonosz Bajtazar codziennie musi odwiedzić wszystkie ulice swojego
rejonu i dostarczyć listy.
Wszystkie ulice są jednokierunkowe i łączą (parami różne) skrzyżowania.
Parę skrzyżowań mogą łączyć co najwyżej dwie ulice: jedna w jednym,
a druga w drugim kierunku.
Skrzyżowania są ponumerowane od 1 do  .
.
Bajtazar rozpoczyna i kończy trasę w centrali poczty Bajtockiej, przy skrzyżowaniu nr 1. Od dawien dawna Bajtazar sam wybierał trasę, którą obchodził swój rejon, jednak ostatnio dyrekcja poczty wydała nowe rozporządzenie, ograniczające swobodę wyboru tras. Każdemu listonoszowi przydzielono pewien zestaw fragmentów trasy - zbiór sekwencji skrzyżowań. Bajtazar musi wybrać taką trasę, która:
- prowadzi każdą ulicą dokładnie raz,
- zawiera w sobie każdą z zadanych sekwencji (jako spójny podciąg),
- rozpoczyna się i kończy na skrzyżowaniu nr 1.
Zadanie
Napisz program który:
- wczyta ze standardowego wejścia opis ulic i przydzielone sekwencje,
- sprawdzi czy Bajtazar może obejść swój rejon, tak żeby odwiedzić każdą ulicę dokładnie raz oraz spełnić wszystkie zalecenia dyrekcji,
- wypisze na standardowe wyjście znalezioną trasę lub stwierdzi że taka trasa nie istnieje.
Wejście
W pierwszym wierszu standardowego wejścia
zapisanie są dwie liczby całkowite  i
i 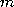 oddzielone pojedynczym odstępem,
oddzielone pojedynczym odstępem,
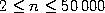 ,
,  ,
odpowiednio liczba skrzyżowań i ulic.
W kolejnych
,
odpowiednio liczba skrzyżowań i ulic.
W kolejnych 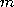 wierszach znajdują się opisy ulic:
dwie liczby całkowite
wierszach znajdują się opisy ulic:
dwie liczby całkowite  ,
, 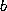 , oddzielone
pojedynczym odstępem,
, oddzielone
pojedynczym odstępem, 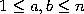 ,
, 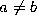 , oznaczają, że
ze skrzyżowania
, oznaczają, że
ze skrzyżowania  do
do 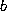 prowadzi (jednokierunkowa) ulica.
Każda (uporządkowana) para
prowadzi (jednokierunkowa) ulica.
Każda (uporządkowana) para 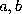 pojawia się w danych co najwyżej raz.
W kolejnym wierszu zapisana jest liczba
pojawia się w danych co najwyżej raz.
W kolejnym wierszu zapisana jest liczba 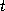 ,
,  ,
oznaczająca liczbę nakazanych sekwencji.
W kolejnych
,
oznaczająca liczbę nakazanych sekwencji.
W kolejnych 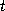 wierszach zapisane są opisy sekwencji.
Opis sekwencji składa się z liczby
wierszach zapisane są opisy sekwencji.
Opis sekwencji składa się z liczby 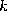 ,
, 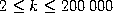 ,
oraz ciągu
,
oraz ciągu 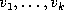 numerów skrzyżowań.
Liczby w wierszu są pooddzielane pojedynczymi odstępami.
Sumaryczna długość wszystkich sekwencji nie przekracza
numerów skrzyżowań.
Liczby w wierszu są pooddzielane pojedynczymi odstępami.
Sumaryczna długość wszystkich sekwencji nie przekracza 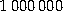 .
.
Wyjście
Twój program powinien wypisać w pierwszym wierszu wyjścia:
- TAK - jeśli istnieje trasa spełniająca warunki zadania,
- NIE - jeśli taka trasa nie istnieje.
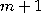 liczb:
liczb: 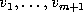 ,
każdej wypisanej w osobnym wierszu, takich że:
,
każdej wypisanej w osobnym wierszu, takich że:
-
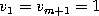 ,
, -
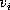 i
i 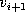 (dla
(dla 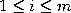 ) są połączone ulicami,
) są połączone ulicami, - każda ulica występuje na liście dokładnie raz,
- trasa zawiera, jako spójne podciągi, wszystkie nakazane przez dyrekcję sekwencje.
Przykład
Dla danych wejściowych:
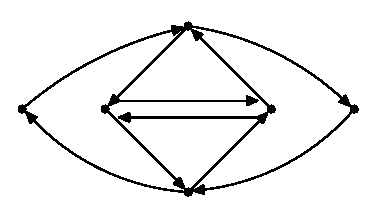
6 10 1 5 1 3 4 1 6 4 3 6 3 4 4 3 5 6 6 2 2 1 4 3 1 5 6 3 3 4 3 4 4 3 6 4 3 5 6 2
poprawną odpowiedzią jest:
TAK 1 3 4 3 6 4 1 5 6 2 1
Autor zadania: Tomasz Waleń.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English