
Zadanie Rekurencyjna mrówka (rek)
Pomóż nam usprawnić bazę zadań!
Rekurencyjna mrówka
Limit pamięci: 32 MB
Mrówka ma obejść wszystkie pola szachownicy 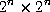 poza polami zabronionymi — każde pole dokładnie jeden raz.
Obchodzenie musi się zacząć w polu startowym leżącym w lewym górnym rogu i zakończyć na polu leżącym na brzegu szachownicy
(mrówka na końcu opuszcza szachownicę).
Zakładamy, że pole startowe nie jest zabronione.
W jednym kroku mrówka może przejść do jednego z co najwyżej czterech sąsiednich pól szachownicy (w górę, dół, lewo lub prawo).
poza polami zabronionymi — każde pole dokładnie jeden raz.
Obchodzenie musi się zacząć w polu startowym leżącym w lewym górnym rogu i zakończyć na polu leżącym na brzegu szachownicy
(mrówka na końcu opuszcza szachownicę).
Zakładamy, że pole startowe nie jest zabronione.
W jednym kroku mrówka może przejść do jednego z co najwyżej czterech sąsiednich pól szachownicy (w górę, dół, lewo lub prawo).
Mrówka obchodzi szachownicę w sposób w pewnym sensie rekurencyjny: aby obejść kwadrat 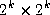 dzieli go na cztery części
(rekurencyjne ćwiartki) o rozmiarach
dzieli go na cztery części
(rekurencyjne ćwiartki) o rozmiarach 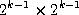 , a następnie obchodzi każdą z nich, to znaczy,
jeżeli mrówka wejdzie do jednej z ćwiartek, to może z niej wyjść dopiero wtedy, gdy obejdzie wszystkie nie zabronione pola w tej ćwiartce.
, a następnie obchodzi każdą z nich, to znaczy,
jeżeli mrówka wejdzie do jednej z ćwiartek, to może z niej wyjść dopiero wtedy, gdy obejdzie wszystkie nie zabronione pola w tej ćwiartce.
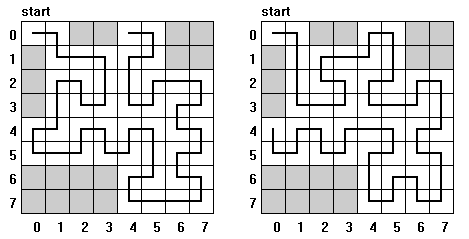
Rysunek przedstawia dwie trasy rekurencyjnej wędrówki mrówki na szachownicy o rozmiarach 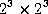 ,
od pola startowego
,
od pola startowego  do pola leżącego odpowiednio na górnym oraz lewym brzegu szachownicy.
do pola leżącego odpowiednio na górnym oraz lewym brzegu szachownicy.
Zadanie
Napisz program, który:
- wczytuje ze standardowego wejścia liczbę całkowitą dodatnią
 określającą jednoznacznie rozmiar szachownicy
określającą jednoznacznie rozmiar szachownicy
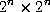 oraz liczbę
oraz liczbę 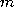 pól zabronionych i ich listę,
pól zabronionych i ich listę,
- na każdym z czterech brzegów szachownicy znajduje pole, na którym może się zakończyć rekurencyjna wędrówka mrówki, spełniająca podane wyżej warunki lub stwierdza, że takiego pola nie ma,
- zapisuje wyniki na standardowe wyjście.
Uwaga: każde z czterech pól narożnych należy do dwóch brzegów szachownicy.
Wejście
W pierwszym wierszu standardowego wejścia jest zapisana liczba całkowita dodatnia  ,
, 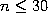 .
W drugim wierszu jest zapisana liczba pól zabronionych
.
W drugim wierszu jest zapisana liczba pól zabronionych  ,
, 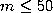 .
.
W każdym z kolejnych 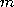 wierszy jest zapisana para liczb całkowitych nieujemnych
wierszy jest zapisana para liczb całkowitych nieujemnych 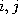 oddzielonych pojedynczym odstępem,
są to dwie współrzędne: numer wiersza
oddzielonych pojedynczym odstępem,
są to dwie współrzędne: numer wiersza 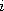 oraz numer kolumny
oraz numer kolumny 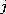 odpowiedniego zabronionego pola.
Wiersze szachownicy numerujemy od góry w dół, a kolumny od lewej do prawej, od
odpowiedniego zabronionego pola.
Wiersze szachownicy numerujemy od góry w dół, a kolumny od lewej do prawej, od 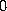 do
do  .
.
Wyjście
W każdym z czterech kolejnych wierszy standardowego wyjścia należy zapisać dwie liczby całkowite nieujemne oddzielone pojedynczym odstępem — współrzędne (numer wiersza i numer kolumny) odpowiedniego końcowego pola rekurencyjnej trasy mrówki leżącego na: górnym, prawym, dolnym oraz lewym brzegu szachownicy (w takiej kolejności) lub jedno słowo NIE, jeśli takiego pola nie ma.
Przykład
Dla danych wejściowych:
3 17 2 0 1 0 3 0 6 0 7 0 6 1 7 1 6 2 7 2 6 3 7 3 0 2 0 3 0 6 0 7 1 6 1 7
poprawną odpowiedzią jest:
0 4 NIE NIE 4 0
Autor zadania: Wojciech Rytter.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English