
Zadanie Czekolada (cze)
Pomóż nam usprawnić bazę zadań!
Czekolada
Limit pamięci: 64 MB
Bituś i Bajtuś dostali od mamy tabliczkę czekolady.
Czekolada jest prostokątem o wymiarach 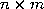 , podzielonym na
, podzielonym na 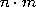 kwadratowych cząstek.
Zamiast po prostu podzielić się nią po połowie, postanowili zagrać w nowo wymyśloną grę.
Oznaczyli pewną losowo wybraną cząstkę krzyżykiem i ustalili następujące zasady:
będą wykonywać na przemian ruchy (Bituś zaczyna); każdy ruch polega na przełamaniu
czekolady wzdłuż jednej z linii (poziomej lub pionowej) oddzielającej cząstki
i zjedzeniu jednej z powstałych w ten sposób części.
Ten, kto zje oznaczoną cząstkę, przegrywa.
kwadratowych cząstek.
Zamiast po prostu podzielić się nią po połowie, postanowili zagrać w nowo wymyśloną grę.
Oznaczyli pewną losowo wybraną cząstkę krzyżykiem i ustalili następujące zasady:
będą wykonywać na przemian ruchy (Bituś zaczyna); każdy ruch polega na przełamaniu
czekolady wzdłuż jednej z linii (poziomej lub pionowej) oddzielającej cząstki
i zjedzeniu jednej z powstałych w ten sposób części.
Ten, kto zje oznaczoną cząstkę, przegrywa.
Gra była bardzo emocjonująca i zakończyła się zwycięstwem Bajtusia.
Niepocieszony Bituś zastanawia się na ile wybór oznaczonego pola miał wpływ na jego przegraną.
Chciałby więc wiedzieć, ile spośród 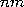 cząstek czekolady
ma tę własność, że przy ich oznaczeniu Bituś przegra.
Zakładamy, że obaj chłopcy grają optymalnie.
cząstek czekolady
ma tę własność, że przy ich oznaczeniu Bituś przegra.
Zakładamy, że obaj chłopcy grają optymalnie.
Wejście
W pierwszym wierszu wejścia znajduje się jedna liczba całkowita 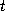 (
( )
oznaczająca liczbę przypadków testowych.
W kolejnych
)
oznaczająca liczbę przypadków testowych.
W kolejnych 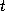 wierszach znajdują się po dwie liczby całkowite
wierszach znajdują się po dwie liczby całkowite
 ,
, 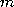 (
(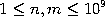 ) oznaczające wymiary tabliczki czekolady.
) oznaczające wymiary tabliczki czekolady.
Wyjście
Na wyjściu należy zapisać dokładnie 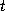 wierszy z odpowiedziami
do kolejnych testów z wejścia: w
wierszy z odpowiedziami
do kolejnych testów z wejścia: w 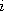 -tym wierszu należy zapisać jedną liczbę całkowitą,
oznaczającą liczbę cząstek czekolady, których oznaczenie na
-tym wierszu należy zapisać jedną liczbę całkowitą,
oznaczającą liczbę cząstek czekolady, których oznaczenie na 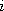 -tej czekoladzie z wejścia prowadzi do przegranej Bitusia.
-tej czekoladzie z wejścia prowadzi do przegranej Bitusia.
Przykład
Dla danych wejściowych:
2 1 2 2 6
poprawną odpowiedzią jest:
0 4
Autor zadania: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English