
Zadanie Słowa (slo)
Pomóż nam usprawnić bazę zadań!
Słowa
Limit pamięci: 32 MB
Na potrzeby tego zadania słowem nazwiemy niepusty ciąg wielkich liter alfabetu angielskiego.
Długością słowa jest liczba zawartych w nim liter.
Tak więc 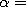 ABAACBBBA jest przykładem słowa o długości 9.
Blokiem w słowie nazywamy maksymalny, spójny podciąg takich samych liter.
Powiemy, że słowo jest
ABAACBBBA jest przykładem słowa o długości 9.
Blokiem w słowie nazywamy maksymalny, spójny podciąg takich samych liter.
Powiemy, że słowo jest 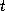 -trudne, jeśli zawiera
-trudne, jeśli zawiera 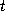 bloków.
Nasze przykładowe słowo
bloków.
Nasze przykładowe słowo  jest 6-trudne, ponieważ składa się z bloków A|B|AA|C|BBB|A.
jest 6-trudne, ponieważ składa się z bloków A|B|AA|C|BBB|A.
Jeśli dwa słowa mają taką samą długość, to możemy badać, jak bardzo się różnią.
Dwa słowa o długości  są
są  -niepodobne, jeśli dla dokładnie
-niepodobne, jeśli dla dokładnie  indeksów
indeksów 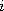 (
(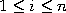 ),
), 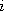 -ta litera pierwszego słowa jest inna niż
-ta litera pierwszego słowa jest inna niż 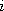 -ta litera drugiego słowa.
Jeśli weźmiemy słowo
-ta litera drugiego słowa.
Jeśli weźmiemy słowo  AAAABBBBB, to słowa
AAAABBBBB, to słowa  i
i 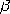 są 3-niepodobne.
są 3-niepodobne.
Dla danego słowa  , chcemy znaleźć niezbyt różniące się od niego słowo
, chcemy znaleźć niezbyt różniące się od niego słowo 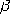 ,
które nie będzie na dodatek zbyt trudne. Twoim zadaniem będzie stwierdzić na ile łatwe może być słowo
,
które nie będzie na dodatek zbyt trudne. Twoim zadaniem będzie stwierdzić na ile łatwe może być słowo 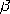 .
.
Zadanie
Napisz program, który:
-
wczyta liczby
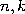 i słowo
i słowo  o długości
o długości  ;
;
-
wyznaczy minimalne
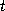 , takie że istnieje słowo
, takie że istnieje słowo 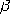
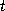 -trudne, które jest co najwyżej
-trudne, które jest co najwyżej 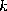 -niepodobne do wczytanego
słowa
-niepodobne do wczytanego
słowa  (to znaczy, że nie istnieje
(to znaczy, że nie istnieje 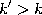 takie, że słowa
takie, że słowa  i
i 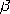 są
są  -niepodobne);
-niepodobne);
- wypisze wynik.
Wejście
W pierwszym wierszu wejścia znajdują się dwie liczby całkowite 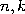 oddzielone pojedynczym odstępem
(
oddzielone pojedynczym odstępem
(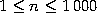 ,
, 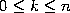 ). Oznaczają one odpowiednio: długość słowa
). Oznaczają one odpowiednio: długość słowa  i dopuszczalny stopień
niepodobieństwa. W drugim wierszu znajduje się
i dopuszczalny stopień
niepodobieństwa. W drugim wierszu znajduje się  -literowe słowo
-literowe słowo  złożone z wielkich liter alfabetu angielskiego.
złożone z wielkich liter alfabetu angielskiego.
Wyjście
W jedynym wierszu wyjścia należy wypisać szukaną liczbę 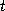 .
.
Przykład
Dla danych wejściowych:9 3 ABAACBBBApoprawną odpowiedzią jest:
2
Autor zadania: Tomasz Idziaszek.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English