
Zadanie Odcinki (odc)
Pomóż nam usprawnić bazę zadań!
Odcinki
Limit pamięci: 32 MB
Rozważmy zbiór 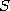 składający się z
składający się z  domkniętych (zawierających końce)
pionowych odcinków na płaszczyźnie.
Żadne dwa odcinki ze zbioru
domkniętych (zawierających końce)
pionowych odcinków na płaszczyźnie.
Żadne dwa odcinki ze zbioru 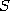 nie mają
wspólnych punktów.
Mówimy, że dwa odcinki z
nie mają
wspólnych punktów.
Mówimy, że dwa odcinki z 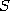 się widzą, jeżeli istnieje poziomy
odcinek, który je łączy i nie ma punktów wspólnych z żadnymi innymi
odcinkami ze zbioru
się widzą, jeżeli istnieje poziomy
odcinek, który je łączy i nie ma punktów wspólnych z żadnymi innymi
odcinkami ze zbioru 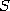 .
.
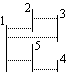
Na poniższym rysunku znajduje się przykładowy zbiór odcinków. Pary widzących się odcinków to: 1-2, 1-3, 2-3, 1-5 i 4-5. Odcinki 1 i 4 się nie widzą.
Dla danej liczby  , poszukujemy
, poszukujemy  -elementowego zbioru pionowych
odcinków, w którym jak najwięcej par odcinków się widzi.
-elementowego zbioru pionowych
odcinków, w którym jak najwięcej par odcinków się widzi.
Zadanie
Napisz program, który:
-
wczyta ze standardowego wejścia liczbę
 ,
,
-
wyznaczy takie ułożenie
 pionowych odcinków, że:
pionowych odcinków, że:
- żadne dwa z nich nie mają wspólnych punktów,
- liczba par spośród nich, które się widzą jest maksymalna,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy i jedyny wiersz wejścia zawiera jedną liczbę całkowitą
 (
(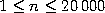 ) - liczbę odcinków w poszukiwanym zbiorze.
) - liczbę odcinków w poszukiwanym zbiorze.
Wyjście
Pierwszy wiersz wyjścia powinien zawierać jedną liczbę całkowitą -
maksymalną liczbę par widzących się odcinków.
Kolejnych  wierszy powinno opisywać odpowiednie rozmieszczenie
odcinków - po jednym odcinku w wierszu.
Wiersz
wierszy powinno opisywać odpowiednie rozmieszczenie
odcinków - po jednym odcinku w wierszu.
Wiersz 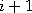 -szy (dla
-szy (dla 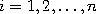 ) powinien zawierać trzy
liczby całkowite:
) powinien zawierać trzy
liczby całkowite:
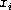 ,
, 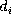 i
i 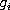 (
(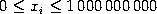 ,
,
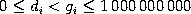 ),
pooddzielane pojedynczymi odstępami i opisujące
odcinek o końcach
),
pooddzielane pojedynczymi odstępami i opisujące
odcinek o końcach 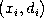 i
i 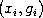 .
.
Jeżeli istnieje wiele poprawnych rozmieszczeń  odcinków, to Twój
program może wypisać dowolne z nich.
odcinków, to Twój
program może wypisać dowolne z nich.
Dla danych wejściowych:
4poprawną odpowiedzią jest:
6 1 1 5 2 2 4 3 3 5 4 1 4
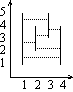
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English