
Kontakt
W razie problemów technicznych ze Szkopułem, prosimy o kontakt mailowy pod adresem [email protected].
Jeśli chciałbyś porozmawiać o zadaniach, rozwiązaniach lub problemach technicznych, zapraszamy na serwery Discord. Są one moderowane przez społeczność, ale członkowie zespołu technicznego też są tam aktywni.
Zadanie Squarki (squ)
Pomóż nam usprawnić bazę zadań!
Squarks
Memory limit: 64 MB
A famous Byteotian physicist Byteasar is studying a new constituent of matter - squarks. These are quite exotic particles that never exist alone but always in pairs. Moreover, squarks of a particular kind form pairs only with squarks of different kinds.
After years of studies Byteasar has established that there are  different kinds of squarks.
Squarks of each kind have a unique mass, which is a positive integer multiple of (an appropriate) unit.
Byteasar has also measured the total mass of each of the
different kinds of squarks.
Squarks of each kind have a unique mass, which is a positive integer multiple of (an appropriate) unit.
Byteasar has also measured the total mass of each of the 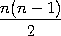 possible pairs of squarks.
According to standard Byteotian model of physics, the mass of a pair of squarks equals the sum of the masses
of the two squarks forming it.
possible pairs of squarks.
According to standard Byteotian model of physics, the mass of a pair of squarks equals the sum of the masses
of the two squarks forming it.
Now Byteasar desires to determine the individual masses of squarks of every kind. He has asked your help in writing a program that will determine all solutions to this puzzle, i.e., will reconstruct all configurations of squark masses that are consistent with his previous measurements.
Input
In the first line of the standard input there is a single integer  (
(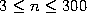 )
that denotes the number of different kinds of squarks.
In the second line there are
)
that denotes the number of different kinds of squarks.
In the second line there are 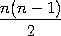 positive integers, separated by single spaces,
that denote the total masses of all possible pairs of squarks.
The mass of every pair does not exceed
positive integers, separated by single spaces,
that denote the total masses of all possible pairs of squarks.
The mass of every pair does not exceed 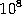 .
For each two different kinds of squarks, the mass of the pair they form is given on the input exactly once.
The masses on the input are given in a random order.
.
For each two different kinds of squarks, the mass of the pair they form is given on the input exactly once.
The masses on the input are given in a random order.
In tests worth 32% of the points the following conditions hold in addition:
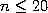 and the mass of every pair of squarks does not exceed
and the mass of every pair of squarks does not exceed 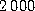 .
.
Output
In the first line of the standard output your program should print the number 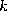 of possible solutions to the problem.
In the
of possible solutions to the problem.
In the 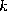 lines that follow it should report successive solutions, one per line.
Each solution should consist of
lines that follow it should report successive solutions, one per line.
Each solution should consist of  different positive integers, namely the masses of squarks of all kinds.
In every solution these should be given in increasing order and separated by single spaces.
different positive integers, namely the masses of squarks of all kinds.
In every solution these should be given in increasing order and separated by single spaces.
Solutions can be reported in arbitrary order, but they cannot be repeated.
You may assume that for each test data there exists at least one solution, i.e., 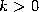 .
.
Example
For the input data:
4 3 5 4 7 6 5
the correct result is:
1 1 2 3 4
whereas for the following input data:
4 11 17 12 20 21 15
a correct result is:
2 4 7 8 13 3 8 9 12
Task author: Jakub Onufry Wojtaszczyk.

 English
English